| inf | Дата: Четверг, 30.10.2014, 07:23 | Сообщение # 16 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке К. Найдите площадь параллелограмма, если ВС = 2, а расстояние от точки К до стороны АВ равно 1.
Решение:
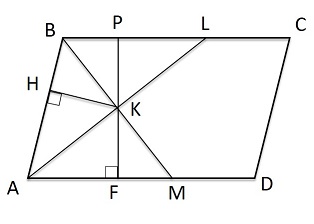
1) KH - расстояние от точки К до стороны АВ ⇒ KH = 1
2) Δ ABL - равнобедренный (∠ BAL = ∠ BLA) ⇒ AB = ВL и ∠ AВК = ∠ LВК;
аналогично из треугольника ВМА AB = АМ и ∠ AВК = ∠ АМК ⇒ Δ BLK = Δ BAK = Δ MAK ⇒ KH = KF = KP ⇒ PF = 2
3) SABCD = BC · PF = 4
Ответ: 4
|
| |
| |
| Алена | Дата: Четверг, 20.11.2014, 20:03 | Сообщение # 17 |
|
Группа: Гости
| ВМ -медиана А(1; 0), В (-2;-3), С (0; 5)
1) М (?)
2) у=кх+в
3) А В С
|
| |
| |
| inf | Дата: Вторник, 02.12.2014, 18:42 | Сообщение # 18 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Здравствуйте,
Username: nataannaeva
Название формы: Обратная связь
========================================
Имя отправителя: Наталья
Текст сообщения:
-----------------
В треугольнике АВС через вершину А проведена окружность касающаяся стороны ВС в вершине С и пересекающая сторону АВ в точке D.Найдите длину стороны АВ , если АD=16, и АС:СD=3:1. Почему треугольник АВС прямоугольный? Центр окружности- это пересечение серединного перпендикуляра стороны АС и перпендикуляра к стороне ВС, проведенного к точке С. Вы рассматриваете частный случай- когда АС лежит на диаметре пенпердикулярном ВС. А если АД- это диаметр? АС может лежать выше диаметра окружности, ниже. Можете объяснить, почему АВС прямоугольный ? Это за�
�ача
9-го класса, если АВС-прямоугольный, то можно решить через подобие, намного легче. Как доказать, что АВС- прямоугольный я не знаю. Если Вы мне напишите, то заранее огромное спасибо. Наталья.
-----------------
Оценка сайта: Отлично
IP: 95.128.243.5
Дата: 02.12.2014, 07:50
========================================
Всего наилучшего.
Ответ:
Да, конечно, мною рассмотрен частный случай. Когда эта задача мне попалась первично, рассматривала все варианты для треугольника АВС: остроугольный, прямоугольный и тупоугольный. Поскольку с прямоугольным треугольником решается "на раз" это решение и выложила.
--
Н.Ф. Ишутченко
|
| |
| |
| Гость | Дата: Понедельник, 08.12.2014, 12:06 | Сообщение # 19 |
|
Группа: Гости
| спасибо, очень подробное решение и грамотное
|
| |
| |
| гость | Дата: Воскресенье, 11.01.2015, 16:57 | Сообщение # 20 |
|
Группа: Гости
| медиана ВМ и бессектриса АР треугольника АВС пересекаются в точке К, длина стороны АС относится к длине стороны АВ как 6:7. Найдите отношение площади треугольника ВКР к площади четырёхугольника КРСМ
|
| |
| |
| Гость | Дата: Воскресенье, 11.01.2015, 16:58 | Сообщение # 21 |
|
Группа: Гости
| окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности , если АВ=8, АС=10
|
| |
| |
| Гость | Дата: Среда, 04.02.2015, 19:13 | Сообщение # 22 |
|
Группа: Гости
| Дана прямоугольная трапеция, АВ перпендикулярно АД, ВС=14, АД=15. Окружность проходит через точки С и Д, а также касается стороны АВ. Найти расстояние от точки касания до прямой СД.
|
| |
| |
| Гость | Дата: Понедельник, 16.03.2015, 21:55 | Сообщение # 23 |
|
Группа: Гости
| В окружность с центром О вписали трапецию АВСD, в которой сторона АВ параллельна стороне СD, АВ=8, СD=3, ∠ABC=60.Точка К лежит на отрезае АВ, причём АК=2. прямая СК пересекакт окружность в точке F,отличной С. Найдите площадь треугольника ОFС. 
|
| |
| |
| Гость | Дата: Четверг, 19.03.2015, 16:59 | Сообщение # 24 |
|
Группа: Гости
| Треугольник задан координатами своих вершин. Найдите внутренний угол при вершине А, длину медианы ВМ, площадь треугольника АВС и длину высоты СН
А(9;1;3) В (2;-1;3) С (-4;1;5)
|
| |
| |