| inf | Дата: Воскресенье, 16.06.2013, 07:57 | Сообщение # 1 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Обсуждаем задания
Вы можете добавлять ответы в качестве гостей сайта, но для того чтобы иметь возможность прикрепить файл к своему сообщению, необходимо зарегистрироваться.
Пожалуйста, называйте себя при создании сообщения в качестве гостей сайта. Все "неопознанные" сообщения будут удалены, также будут удалены сообщения, нарушающие правила сайта, содержащие ненормативную лексику, пропаганду насилия и прочую подобную ассоциальность, содержащие оскорбления и др. Вобщем, будьте взаимовежливы!!!
|
| |
| |
| inf | Дата: Понедельник, 07.04.2014, 08:34 | Сообщение # 2 |
|
Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Срезовая работа по модулю геометрия от 03(04).04.14
1. В треугольнике АВС угол С прямой, АС = 8, cosА = 0,4
Найти АВ.
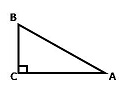
Решение: косинус - это отношение прилежащего катета к гипотенузе.
cosА = АС/АВ ⇒ АВ = АС/cosA ⇒ АВ = 8/0,4 = 20
Ответ: 20
2. Центральный угол АОВ равный 600, опирается на хорду АВ длиной 3. Найдите радиус окружности.
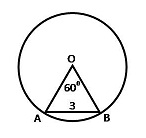 Решение: т.к. центральный угол АОВ равен 600, то треугольник, образованный его сторонами и хордой, на которую он опирается (Δ АОВ), является равносторонним ⇒ АО = АВ = 3
Ответ: 3
3. В ромбе сторона равна 10, одна из диагоналей - 10√3,а угол , лежащий напротив этой диагонали, равен 1200. Найдите площадь ромба, деленную на √3.
Решение: Данных более, чем предостаточно, площадь ромба в этом случае можно найти по любой известной Вам формуле. Самая очевидна: S = ab*sinα
S = 10*10*sin1200 = 100*√3/2=50√3
Ответ: 50
4. На рисунке изображена трапеция АВСD. Используя рисунок, найдите sinА
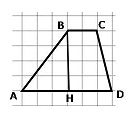
Решение: По теореме Пифагора находим гипотенузу прямоугольного треугольника АВН АВ = 5. Синус - это отношение противолежащего катета к гипотенузе:
sinА = ВН/АВ = 4/5 = 0,8
Ответ: 0,8
5. Укажите номера верных утверждений:
1) Площадь трапеции равна половине высоты, умноженнойна разность оснований.
2) Через любые две точки можно провести прямую.
3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.
Ответ: 2;3
|
| |
| |
| inf | Дата: Среда, 09.04.2014, 09:37 | Сообщение # 3 |
|
Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 1. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 300 и 800 соответственно.
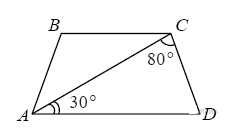
Решение: Угол САD равен углу АСВ (накрестлежащие) ⇒ угол С трапеции равен 1100. Т.к. трапеция является равнобедренной, то и угол АВС равен 1100.
Ответ: 110
2. В равностороннем треугольнике АВС биссектрисы CN и АМ пересекаются в точке Р. Найдите угол МРN.
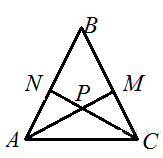
Решение: Т.к. CN и АМ – биссектрисы, то в треугольнике АРС сумма углов А и С равна 600 (каждый из них равен по 300) ⇒ угол АРС равен 1200. Углы АРС и NPM вертикальные ⇒ угол NPM равен 1200.
Ответ: 120
3. Радиус ОВ окружности с центром в точке О пересекает хорду АС в точке D и перпендикулярен ей. Найдите длину хорды АС, если BD = 1 см, а радиус окружности равен 5 см.
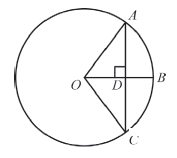
Решение: треугольник АОС равнобедренный ⇒ OD – высота и медиана. В прямоугольном треугольнике AOD по теореме Пифагора находим AD = 3 (АО = 5, OD = OB – BD = 4) ⇒ АС = 6.
Ответ: 6
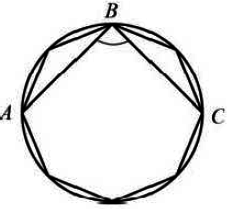
4. В окружность вписан равносторонний восьмиугольник. Найдите величину угла АВС.
Решение: Угол АВС – вписанный в окружность. Т.к. угол АВС опирается на диаметр АС ⇒ равен 900.
Ответ: 90
5. В треугольнике АВС угол С равен 900, ВС = 12, sinА = 4/11. Найдите АВ.
Решение: синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе: sinA = BC/AB ⇒ AB = BC/sinA ⇒ АВ = 33
Ответ: 33
6. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 300. Найдите площадь прямоугольника, деленную на √3.
Решение: По определению прямоугольника все его углы прямые. Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Таким образом, одна из сторон прямоугольника равна 5. По теореме Пифагора найдем вторую строну: 5√3
Площадь прямоугольника равна произведению его сторон, имеем:
S = 5∙5√3 = 25√3
Ответ: 25
7. На рисунке изображен ромб ABCD. Используя рисунок, найдите тангенс угла ОВС.
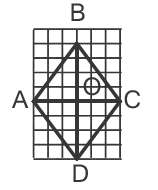
Решение:
Тангенс угла прямоугольного треугольника равен отношению противолежжащего катета к прилежащему: 3 клетки/4 клетки = 0,75
Ответ: 0,75
8. На рисунке изображен прямоугольный треугольник. Найдите длину медианы треугольника, проведенную из вершины прямого угла.
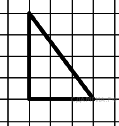
Решение: медиана прямоугольного треугольника, проведенная из вершины прямого угла равна половине его гипотенузы. По теореме Пифагора находим гипотенузу, равна 5 клеткам, т.к. катеты равны 3 и 4 клетки. Медиана равна 2,5.
9. На рисунке изображен график функции y = f(x). Укажите номера НЕверных утверждений.
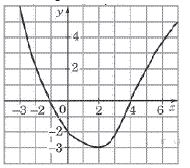
1) Функция возрастает на промежутке [- 2; + )
2) f(3) > f(- 3)
3) f(0) = - 2
4) Прямая у = 2 пересекает график функции в точках (- 2; 2) и (5; 2)
Ответ: 1, 2
10. Какие из следующих высказываний верны?
1) В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол А – наибольший.
2) Каждая сторона треугольника не превосходит суммы двух других его сторон.
3) Если два треугольника подобны, то их соответствующие стороны равны.
4) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.
Ответ: 2
|
| |
| |
| cesal43288 | Дата: Вторник, 27.02.2024, 14:29 | Сообщение # 4 |
|
Рядовой
Группа: Пользователи
Сообщений: 1
Статус: Offline
| 
|
| |
| |
