|
Задания 21.
|
|
| inf | Дата: Воскресенье, 12.01.2014, 07:31 | Сообщение # 1 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Учимся решать 21 задания.
|
| |
|
|
| inf | Дата: Воскресенье, 12.01.2014, 07:32 | Сообщение # 2 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 1. Сократите дробь
Поработаем со знаменателем дроби
Сократим дробь на 2n и вычислим.
Ответ: 4
|
| |
|
|
| inf | Дата: Пятница, 16.05.2014, 07:45 | Сообщение # 3 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Упростите выражение (m - 2)/(m2 - m - 2) - m/(m2 + 2m + 1).
Решение:
(m - 2)/(m2 - m - 2) - m/(m2 + 2m + 1) = (m - 2)/(m + 1)(m - 2) - m/(m + 1)2 = 1/(m + 1) - m/(m + 1)2=(m + 1 - m)/(m + 1)2 = 1/(m + 1)2
|
| |
|
|
| inf | Дата: Понедельник, 19.05.2014, 09:10 | Сообщение # 4 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 1. Упростите выражение
Ответ: 2,4
|
| |
|
|
| inf | Дата: Воскресенье, 25.05.2014, 12:45 | Сообщение # 5 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Решите неравенство:
х2(- х2 - 64) ≤ 64(- х2 - 64).
Решение:
х2(- х2 - 64) ≤ 64(- х2 - 64);
х2(- х2 - 64) - 64(- х2 - 64) ≤0;
- х2(х2 + 64) + 64(х2 + 64) ≤0;
х2(х2 + 64) - 64(х2 + 64) ≥ 0;
(х2 + 64)(х2 - 64) ≥ 0;
Т.к. (х2 + 64) > 0 при любом значении х, то
х2 - 64 ≥ 0
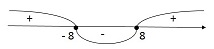
x ∈ (- ∞; - 8) U (8; +∞)
Ответ: x ∈ (- ∞; - 8) U (8; +∞)
|
| |
|
|
| inf | Дата: Понедельник, 26.05.2014, 20:32 | Сообщение # 6 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| | √54 | | √(√(15) - 3)√(√(15) + 3) |
ПО свойству корней "загоняем" все под один корень, в знаменателе применяем разность квадратов: √(54/(15 - 9) = 3
|
| |
|
|
| inf | Дата: Среда, 28.05.2014, 17:00 | Сообщение # 7 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Решите неравенство: (3х - 5)2 ≥ (5х - 3)2 .
(3х - 5)2 - (5х - 3)2 ≥ 0;
((3х - 5) - (5х - 3))((3х - 5) + (5х - 3))≥ 0;//применили разность квадратов
(-2х - 2)(8х - 8) ≥ 0;//раскрыли скобки, привели подобные
-2 . (х + 1) . 8 . (х - 1) ≥ 0;//вынесли общие множители
(х + 1)(х - 1) ≤ 0;//разделили на отрицательное число, знак неравенства поменяли

x ∈ [-1; 1]
Ответ: x ∈ [-1; 1]
|
| |
|
|
| inf | Дата: Среда, 28.05.2014, 17:08 | Сообщение # 8 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Решите систему уравнений: { | (3х + 7у)2 = 10у | | (3х + 7у)2 = 10х |
Замечаем, что левые части уравнений равны, следовательно равны и правые части, т.е. х = у. Подставляем в перое уравнение вместо одной переменной другую:
(3х + 7х)2 = 10х;
100х2 - 10х = 0;
х(10х - 1) = 0;
Ответ: (0; 0); (0,1; 0,1)
|
| |
|
|
| inf | Дата: Пятница, 10.10.2014, 12:48 | Сообщение # 9 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Решите уравнение:
х2 - 6х + √(6 - х)= √(6 - х) + 7
ОДЗ:
6 - х ≥ 0;
х ≤ 6.
х2 - 6х + √(6 - х)= √(6 - х) + 7;
х2 - 6х + √(6 - х) - √(6 - х) - 7 = 0;
х2 - 6х - 7 = 0;
х1 = 7 посторонний корень (не удовлетворяет ОДЗ)
х2 = - 1
Ответ: - 1.
|
| |
|
|
| inf | Дата: Пятница, 24.10.2014, 20:30 | Сообщение # 10 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 21. Вариант № 101 от 31.05.2014 (источник)
(3х - 5)2 ≥ (5х - 3)2;
(3х - 5)2 - (5х - 3)2≥ 0;
(3х - 5 - 5х + 3)(3х - 5 + 5х - 3)≥ 0;
(- 2х - 2)(8х - 8) ≥ 0;
- 2 . 8 . (х + 1)(х - 1)≥ 0;
(х + 1)(х - 1)≤ 0
Ответ: [-1; 1]
|
| |
|
|
| inf | Дата: Суббота, 25.10.2014, 08:58 | Сообщение # 11 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 21. Вариант № 102 от 31.05.2014 (источник)
Решите систему уравнений: { | х2 = 4у + 1 | | х2 + 3 = 4у + у2 |
Решаем методом алгебраической суммы, вычитаем из второго уравнения первое:
3 = у2 - 1;
у = ±2
Эта система решений не имеет
Ответ: (3; 2); (- 3; 2)
|
| |
|
|