|
Задания 25. Геометрические задачи на доказательство.
|
|
| inf | Дата: Воскресенье, 12.01.2014, 07:50 | Сообщение # 1 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Учимся решать задачи на доказательство.
|
| |
| |
| inf | Дата: Понедельник, 07.04.2014, 10:36 | Сообщение # 2 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Два равных прямоугольника имеют общую вершину О
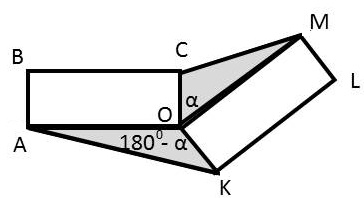
Докажите, что площади треугольников АОК и СОМ равны.
Доказательство:
Пусть угол СОМ равен α, тогда угол АОК равен (1800 - α)
SCOM = 1/2*OC*OM * sinα
SAOK = 1/2*OK*OA*sin(1800-α) = 1/2*OK*OA*sinα = 1/2*OC*OM * sinα = SCOM
Что и требовалось доказать
|
| |
| |
| inf | Дата: Пятница, 16.05.2014, 10:17 | Сообщение # 3 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В параллелограмме АВСD точка М - середина стороны АВ. Известно, что МС = MD. Докажите, что данный параллелограмм - прямоугольник.
Решение:
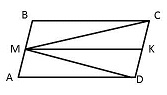
Проведеи МК || AD ⇒ CK = KD, т.е. МК - медиана равнобедренного треугольника CMD ⇒ МК - высота ⇒ МК ⊥ CD ⇒ AD ⊥ CD ⇒ ABCD - прямоугольник.
ч.т.д.
|
| |
| |
| inf | Дата: Понедельник, 19.05.2014, 11:46 | Сообщение # 4 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В окружности через середину хзарды АС проведена хорда BD так, что АВ = CD. Докажите, что О - середина хорды BD.
Решение:
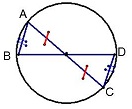
∠ AOD = ∠ DOC (вертикальные) ⇒ дуги ВС и AD равны ⇒ ∠ ВАС = ∠ DCA ⇒ Δ АОВ = Δ СОD ⇒ OB = OD ⇒ О - середина хорды BD.
ч.т.д.
|
| |
| |
| inf | Дата: Вторник, 20.05.2014, 07:02 | Сообщение # 5 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС. Докажите, что BFDE - параллелограмм.
Решение:
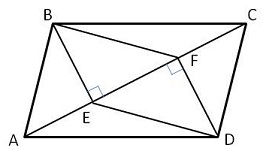
1) Δ АВС = Δ CDA ⇒ BE = FD (как высоты, проведенные к равным сторонам)
2) BE ⊥ АС и FD ⊥ АС ⇒ BE || FD
Из 1) и 2) ⇒ BFDE - параллелограмм.
ч.т.д.
|
| |
| |
| inf | Дата: Вторник, 20.05.2014, 10:39 | Сообщение # 6 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В остроугольном треугольнике АВС проведены высоты СЕ и AD. Докажите, что Δ АВD подобен Δ СВЕ.
Решение:
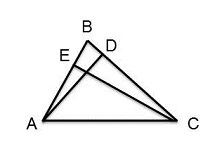
Δ АВD подобен Δ СВЕ по двум углам: треугольники прямоугольные и угол В - общий.
ч.т.д.
|
| |
| |
| inf | Дата: Воскресенье, 25.05.2014, 13:55 | Сообщение # 7 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Известно, что около четырехугольника ABCD можно описать окружность и что продолжения сторон АВ и CD четырехугольника пересекаются в точке М. Докажите, что треугольники МВС и MDA подобны.
Решение:
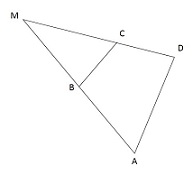
∠ АВС = 1800 - ∠ ADC, т.к. около четырехугольника ABCD можно описать окружность.
∠ МВС = 1800 - ∠ AВC = ∠ ADC и ∠ М - общий для троеугольников МВС и MDA ⇒ Δ МВС ∼ Δ MDA.
ч.т.д.
|
| |
| |
| Гость | Дата: Воскресенье, 25.05.2014, 21:05 | Сообщение # 8 |
|
Группа: Гости
| Спасибо огромнейшее, скажите, а на огэ будут подобные задания?
|
| |
| |
| inf | Дата: Воскресенье, 25.05.2014, 21:18 | Сообщение # 9 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Цитата Гость (  ) Спасибо огромнейшее, скажите, а на огэ будут подобные задания? |
| |
| |
| inf | Дата: Понедельник, 26.05.2014, 16:29 | Сообщение # 10 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В остроугольном треугольнике АВС угол В равен 600. Докажите, что точки А,С, центр описанной около треугольника АВС окружности и точка пересечения его высот лежат на одной окружности.
Решение:
Для доказательства нам понадобятся следующие теоремы:
1. Центр описанной окружности - точка пересечения серединных перпендикуляров к сторонам треугольника;
2. Серединные перпендикуляры треугольника к сторонам треугольника пересекаются в одной точке;
3. Высоты треугольника пересекаются в одной точке.
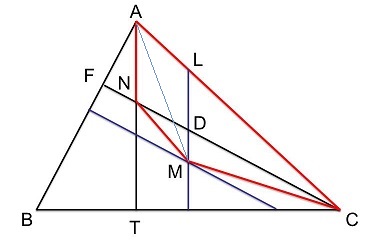
N - точка пересечения высот; М - точка пересечения серединных перпендикуляров. Т.к. треугольник остроугольный, то точки N и М при любой градусной мере углов А и С будут лежать внутри треугольника АВС, т.е. по одну сторону от стороны АС.
По сути, необходимо доказать, что четырехугольник ANMC вписан в окружность, т.е. сумма его противоположных углов равна 1800.
или
Условие принадлежности 4 точек одной окружности.
Если для 4-х точек А,С, М и N выполняется одно из следующих условий:
а) точки М и N расположены по одну сторону от прямой АС и при этом ∠АМС = ∠ANC
б) точки М и N расположены по разные стороны от прямой АС и при этом ∠АМС + ∠ANC = 1800
то эти точки лежат на одной окружности.
Т.о. необходимо доказать, что ∠АМС = ∠ANC, или ∠NАМ = ∠NCМ, или ∠NМС + ∠NАC = 1800 или ∠АNМ + ∠АCМ = 1800.
Доказывать не буду - скучно и сами справитесь: здесь у вас параллельные прямые и целая куча подобных треугольников 
|
| |
| |
| inf | Дата: Среда, 28.05.2014, 18:24 | Сообщение # 11 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| вариант 101 от 31.05.2014 (источник)
Основания ВС и AD трапеции ABCD равны соответственно 5 и 20, BD = 10. Докажите, что треугольники CBD и ADB подобны.
Решение:

CB : BD = 1 : 2 и BD : AD = 1 : 2 и ∠DBC = ∠ BDA ⇒ Δ DBC ∼ Δ BDA.
ч.т.д.
|
| |
| |
| Гость | Дата: Понедельник, 16.06.2014, 20:28 | Сообщение # 12 |
|
Группа: Гости
| Основания ВС и АD трапеции АВСD равны соответственно ВС = 5см, АD = 20см, ВD = 10см. Доказать, что треугольник СВD подобен треугольнику АDВ)А если решить без коэфинцента подобия,а как ВD общая сторона,которая является секущей,и прилежащим к ней накреслежащим углам CBD и BDA.)решение будет верным?)
|
| |
| |
| inf | Дата: Пятница, 10.10.2014, 13:46 | Сообщение # 13 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В равнобедренном треугольнике АВС из концов основания АС проведены прямые, которые составляют с основанием равные углы и пересекаются в точке
К. Докажите равенство треугольников АВК и ВСК.
Решение:
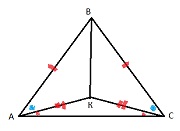
1) АВ = ВС по условию
2) Δ АВС - равнобедренный ⇒ ∠ ВАС = ∠ ВСА ⇒ ∠ ВАК = ∠ ВСК
3) ∠ КАС = ∠ КСА ⇒ Δ АКС - равнобедренный ⇒ АК = КС
Из 1 - 3 ⇒ Δ АВК = Δ ВСК по двум сторонам и углу между ними.
ч.т.д.
|
| |
| |
| inf | Дата: Четверг, 30.10.2014, 06:52 | Сообщение # 14 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Окружности с центрами в точках Е и F пересекаются в точках С и D, причем точки Е и F лежат по одну сторону от прямой СD. Докажите, что СD ⊥ ЕF.
Решение:
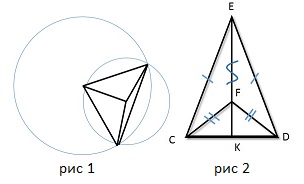
1) CE = ED, CF = FD, EF - общая ⇒ Δ CEF = Δ DEF ⇒ EF - биссектриса, но Δ CED -равнобедренный ⇒ EК - высота, т.е. СD ⊥ ЕF
ч.т.д.
|
| |
| |