|
Задания 23. Построение графиков функций.
|
|
| inf | Дата: Воскресенье, 12.01.2014, 07:42 | Сообщение # 1 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Учимся решать задания № 23.
|
| |
| |
| inf | Дата: Воскресенье, 12.01.2014, 07:42 | Сообщение # 2 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 1. Постройте график функции | y = | x4 - 13x2 + 36 | | (x - 3)(x + 2) |
и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку.
|
| |
| |
| inf | Дата: Понедельник, 07.04.2014, 08:13 | Сообщение # 3 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 1. Постройте график функции | y ={ | -x2 , если |х|≤1 | - 1/х, если |х|
> 1 |
и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку.
Решение:
Промежуток |х|≤1 можно записать в виде x ∈ [- 1; 1]
Промежуток |х|>1 можно записать в виде x ∈ (- ∞; -1)U(1; + ∞)
Строим график
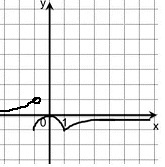
Ответ: с ∈ [0; 1)
|
| |
| |
| inf | Дата: Пятница, 16.05.2014, 08:18 | Сообщение # 4 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Постройте график функции у = х2 - 5х + 10 - 3|х - 2| и найдите все значения а, при которых он имеет ровно три общие точки с прямой у = а + 3.
Решение:
{ | х2 – 5х + 10 – 3х + 6, х ≥ 2 | | х2 – 5х + 10 + 3х – 6, х < 2 |
{ | х2 – 8 х + 16, х ≥ 2 | | х2 – 2х + 4, х < 2 |
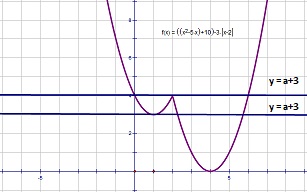
а + 3 = 3
а + 3 = 4
Ответ: При а = 0; а = 1 прямая у = а + 3 имеет с графиком функции ровно три общие точки.
|
| |
| |
| inf | Дата: Вторник, 20.05.2014, 06:21 | Сообщение # 5 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Найдите наименьшее значение выражения и значения x и y, при которых оно достигается:
|3x - 4y - 2| + |x - 5y + 3|
Решение:
Т.к. выражение представляет собой сумму двух неотрицательных выражений, то наименьшее его значение равно 0 и достигается оно тогда и только тогда, когда оба подмодульных выражения равны 0 одновременно.
{ | 3x - 4y - 2 = 0 | | x - 5y + 3 = 0 |
Решаем полученную систему: х = 2, у = 1.
Ответ: наименьшее значение выражения равное 0 достигается при х = 2, у = 1.
|
| |
| |
| inf | Дата: Воскресенье, 25.05.2014, 13:22 | Сообщение # 6 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Постройте график функции
{ | х2 + 4х + 4, х ≥ - 4 | | - 16/х, x < - 4 |
Решение:

Проанализируем, сколько точек пересечения имеет график с прямой y = m, при различных значениях переменной m:
m ∈ (- ∞; 0) - нет точек пересечения
m = 0 - 1 точка
m ∈ (0; 4) - 3 точки
m = 4 - 2 точки
m ∈ (4; + ∞) - 1 точка
Ответ: m ∈ {0} U [4; + ∞)
|
| |
| |
| inf | Дата: Среда, 28.05.2014, 17:34 | Сообщение # 7 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Постройте график функции и определите, при каких значениях параметра k прямая y = kx имеет с графиком ровно одну общую точку.
Решение:
Область определения функции х ≠ 0; х ≠ - 1/9
После преобразований строим график функции у = 1/х и выкалываем точку (-1/9; - 9)
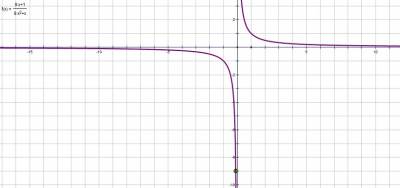
Прямая y = kx имеет с графиком ровно одну общую точку только в случае, когда эта прямая проходит через точку (-1/9; - 9), т.е. k = 81
|
| |
| |
| Гость | Дата: Понедельник, 29.09.2014, 19:10 | Сообщение # 8 |
|
Группа: Гости
| Постройте график функции у=\-2-\х+5\\
|
| |
| |
| inf | Дата: Пятница, 03.10.2014, 13:43 | Сообщение # 9 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Постройте график функции у = |х - 2| - |х + 1| + х - 2 и найдите все значения а, при которых он имеет ровно две общие точки с прямой у = а.
Решение:
На промежутке (- ∞; - 1) оба подмодульные выражения отрицательные, следовательно модули раскроем с противоположными знаками:
у = 2 - х + х + 1 + х - 2 = х + 1
На промежутке [- 1; 2] первое подмодульное выражение отрицательное, второе положительное, следовательно:
у = 2 - х - х - 1 + х - 2 = - х - 1
На промежутке (2; + ∞) оба подмодульные выражения gjkj;bntkmyst, следовательно модули раскроем с противоположными знаками:
у = х - 2 - х - 1 + х - 2 = х - 5
Строим график:

По графику видно, что график функции имеет две точки пересечения с прямой у = 0 и у = - 3
Ответ: - 3; 0
|
| |
| |
| inf | Дата: Пятница, 03.10.2014, 14:05 | Сообщение # 10 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Найдите наибольшее значение выражения

если х и у связаны соотношением: у = х2 + х - 4
Упрощаем выражение:
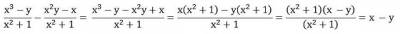
На (х2 + 1) можно сокращать, т.к. это выражение может принимать значения не менее 1 при любом значении х.
Подставляем в полученное выражение заданное соотношение, упрощаем, получаем
В = - х2 + 4
Наибольшее значение полученного выражения равно 4
Ответ: 4
|
| |
| |
| inf | Дата: Пятница, 10.10.2014, 13:19 | Сообщение # 11 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Постройте график функции у = (х2 -3х)·|х|/(х - 3) и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Решение:
у = (х2 -3х)·|х|/(х - 3) = х(х - 3)·|х|/(х - 3) = х·|х|
Строим график функции у= х2, при х < 0; у= - х2, при х ≥ 0; выкалываем точку (3;9), т.к. по области определения х ≠ 3
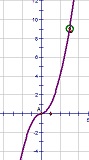
Прямая у = m не будет иметь с графиком функции общих точек только в одном случае при m = 9
Ответ: 9
|
| |
| |
| Гость | Дата: Воскресенье, 12.10.2014, 13:16 | Сообщение # 12 |
|
Группа: Гости
| Постройте график функции:
у={х^2+8х+10 , если х≥-5
{х=у , если х<-5
И определите, при каких значениях m прямая у=m имеет с графиком ровно две точки
|
| |
| |
| inf | Дата: Пятница, 24.10.2014, 10:00 | Сообщение # 13 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Цитата Гость (  ) Постройте график функции: у={х^2+8х+10 , если х≥-5
{х=у , если х<-5
И определите, при каких значениях m прямая у=m имеет с графиком ровно две точки |
| |
| |
| inf | Дата: Пятница, 24.10.2014, 20:52 | Сообщение # 14 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| вариант 101 от 31.05.14 (источник)
Постройте график функции у = (9х + 1)/(9х2 + х) и определите, при каких значениях k прямая у = kх имеет с графиком ровно одну общую точку.
Упростим с учетом ОДЗ (х≠-1/9; х≠ 0)
у = (9х + 1)/(9х2 + х) = (9х + 1)/х(9х + 1) = 1/х
строим график
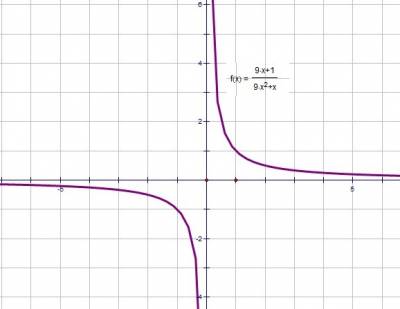
Выкалываем точку (-1/9; -9). Прямая у = kх, проходящая через эту точку будет иметь с графиком функции ровно одну общую точку. Подставляем координаты в уравнение прямой, получаем k = 81.
Ответ: 81
|
| |
| |
| inf | Дата: Суббота, 25.10.2014, 14:38 | Сообщение # 15 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| источник

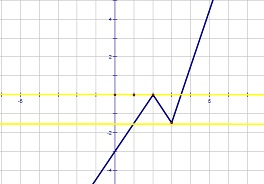
Ответ: 0; - 1,5
|
| |
| |