|
Задания 24. Геометрические задачи на вычисление.
|
|
| inf | Дата: Воскресенье, 12.01.2014, 07:46 | Сообщение # 1 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Решаем 24 задания.
|
| |
| |
| inf | Дата: Воскресенье, 12.01.2014, 07:48 | Сообщение # 2 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 1. В прямоугольном треугольнике АВС с прямым углом С известны катеты: АС = 6, ВС = 8. Найдите медиану СК этого треугольника.
|
| |
| |
| inf | Дата: Понедельник, 07.04.2014, 09:40 | Сообщение # 3 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Диагонали АС и BD трапеции ABCD пересекаются в точке О. Площади трепугольников AOD и ВОС равны соответственно 16 см2 и 9 см2. Найдите площадь трапеции.
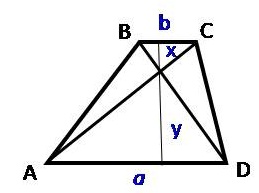
Решение:
1) Δ BOC и Δ AOD подобны ⇒ их площади относятся как коэффициент подобия в квадрате, т.е. коэффициент подобия равен 3/4
Пусть х - высота треугольника ВОС, у - высота треугольника AOD, т.к. коэффициент подобия равен 3/4, то у = 4/3х, а х = 3/4у
2) Площадь трапеции - это произведение полусуммы оснований на высоту (высота трапеции равна сумме высот треугольников АОD и ВОС)
S = 1/2* (a+b)(x+y) = 1/2ax+1/2ay+1/2bx+1/2by = 1/2ax+SAOD+SBOC+1/2by = 1/2a*3/4y+16+9+1/2b*4/3x = 3/4*1/2ay+25+4/3*1/2bx = 25+3/4*SAOD+4/3*SBOC = 25+3/4*16+4/3*9=49
Ответ: 49см2
|
| |
| |
| Элина | Дата: Пятница, 09.05.2014, 15:20 | Сообщение # 4 |
|
Группа: Гости
| Медианы треугольника ABC пересекаются в точке M. Найдите длину медианы, проведённой к стороне BC, если угол BAC равен 47°, а угол BMC равен 133°, BC=4корней из 3.
В этой задаче обязательно до параллелограмма достраивать, или можно решить другим способом без дополнительных построений?
|
| |
| |
| inf | Дата: Понедельник, 12.05.2014, 18:25 | Сообщение # 5 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Цитата Элина ( 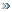 ) Медианы треугольника ABC пересекаются в точке M. Найдите длину медианы, проведённой к стороне BC, если угол BAC равен 47°, а угол BMC равен 133°, BC=4корней из 3. В этой задаче обязательно до параллелограмма достраивать, или можно решить другим способом без дополнительных построений?
Решение:
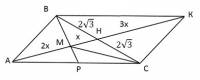
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины, пусть МН = х, тогда АМ = х, АН (искомая медиана) = 3х.
Достроим до параллелограмма АВКС ⇒ ∠А = ∠К = 470.
Рассмотрим четырехугольник ВКСМ.
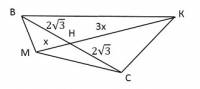
∠М = 1330, ∠К = 470 ⇒возле данного четырехугольника можно описать окружность (сумма противоположных углов равна 1800)
ВС и МК - хорды этой окружности.
ВС ∩ МК = Н ⇒ ВН · НС = МН · НК ⇒ х · 3х = 2√3 · 2√3 ⇒ 3х2 = 12 ⇒ х = 2 ⇒ АН = 6
Ответ: 6
|
| |
| |
| inf | Дата: Пятница, 16.05.2014, 10:00 | Сообщение # 6 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В треугольнике АВС ∠С = 900, радиус вписанной окружности равен 2. Найдите площадь треугольника АВС, если АВ = 12.
Решение:
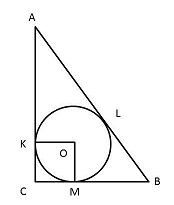
АК = AL, BM = BL, как отрезки касательных проведенных из одной точки ⇒ АК + ВМ = AL + BL = АВ = 12.
КС = МС = r = 2
РАВС = 12 + 12 + 2 + 2 = 28
S = pr = 14 · 2 = 28 ед2
Ответ: 28
|
| |
| |
| inf | Дата: Понедельник, 19.05.2014, 09:38 | Сообщение # 7 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| 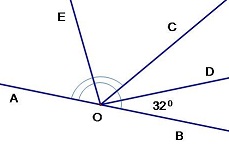
ОЕ - биссектриса угла АОС, ОD- биссектриса угла ВОС. Найдите угол АОЕ, если угол DОВ равен 300
Решение:
OD - биссектриса угла ВОС ⇒ угол ВОС = 640 ⇒ угол АОС равен 1160 (как смежный с углом ВОС) ⇒ угол АОЕ равен 580 (ОЕ - биссектриса угла АОС)
Отве5т: 580
|
| |
| |
| inf | Дата: Вторник, 20.05.2014, 06:44 | Сообщение # 8 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| На сторонах угла ВАС и на его биссектрисе отложены равные отрезки АВ, АС, AD. ∠ BDC = 1600. Определите величину угла ВАС.
Решение:
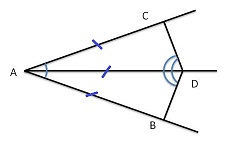
AD биссектриса ⇒ ∠ ADC = 800.
Δ ADC - равнобедренный ⇒ ∠ САD = 200⇒ ∠ ВАС = 400
Ответ: 400
|
| |
| |
| inf | Дата: Воскресенье, 25.05.2014, 13:37 | Сообщение # 9 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Отрезки АВ и CD лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 10, DC = 25, АС = 56.
Решение:

Δ АМВ ∼ Δ CMD ⇒ AM : CM = AB : CD
(56 - х) : х = 10 : 25
х = 40.
Ответ: 40.
|
| |
| |
| inf | Дата: Среда, 28.05.2014, 18:05 | Сообщение # 10 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| вариант 101 от 31.05.14 (источник)
Вершины треугольника делят описанную около треугольника окружность на три дуги, длины которых относятся как 2 : 3 : 7. Найдите радиус окружности, если меньшая из сторон равна 16.
Решение:
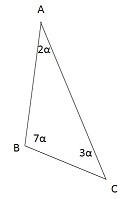
Т.к. длины дуг относятся как 2 : 3 : 7, то в этом же отношении находятся и их градусные меры и градусные меры вписанных углов на них опирающихся, т.е. углов треугольника.
Пусть ∠ А = 2α, тогда ∠ С = 3α, ∠ В = 7α
∠ А + ∠ В +∠ С = 1800 ⇒ 2α + 3α + 7α = 1800 ⇒ 2α = 300
∠ А - наименьший угол треугольника ⇒ ВС = 16
Воспользуемся формулой: a = 2R . sinA
2R . sin300 = 16
R = 16
Ответ: 16
|
| |
| |
| inf | Дата: Среда, 28.05.2014, 18:12 | Сообщение # 11 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Высота АН делит сторону CD ромба ABCD на отрезки DH = 8 и НC = 2. Найдите высоту ромба.
Решение:

Сторона ромба равна 10.
Из прямоугольного треугольника DНА по теореме Пифагора находим высоту.
Ответ: 6
|
| |
| |
| inf | Дата: Пятница, 03.10.2014, 13:50 | Сообщение # 12 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Катет и гипотенуза прямоугольного треугольника равны 18 и 30. Найдите высоту, проведенную к гипотенузе.
Решение:
1) По теореме Пифагора найдем второй катет - 24
2) Катеты прямоугольного треугольника рассмотрим как высоту и основания и найдем площадь: 216
3) Найдем высоту удвоенную площадь раздели на гипотенузу
Ответ: 14,4
РS: можно решить через подобие
|
| |
| |
| inf | Дата: Пятница, 10.10.2014, 13:33 | Сообщение # 13 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Найдите площадь прямоугольного треугольника, если его гипотенуза делится биссектрисой прямого угла на отрезки 15 и 20 см.
Решение:
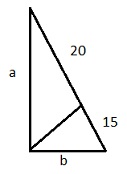
Так как гипотенуза разбита на отрезки биссектрисой, то a/b = 20/15, т.е. на катет а приходится 4 части, на катет b - 3 части. По теореме Пифагора
9х2 + 16х2 = 352
х = 7 ⇒ а = 28, b = 21 ⇒ S = 294
Ответ: 294
|
| |
| |
| inf | Дата: Суббота, 25.10.2014, 14:50 | Сообщение # 14 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| источник
Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведенную к гипотенузе.
Решение:
1. Найдем площадь треугольника: 150
2. Найдем гипотенузу по теореме Пифагора: 25
3. Найдем высоту (удвоенную площадь разделим на гипотенузу): 12
Ответ: 12
Похожая задача
Можно через подобные треугольники.
|
| |
| |