|
Задания 26. Сложные геометрические задачи.
|
|
| inf | Дата: Воскресенье, 12.01.2014, 07:53 | Сообщение # 1 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Решаем геометрические задачи повышенного уровня сложности.
|
| |
| |
| Гость | Дата: Воскресенье, 16.03.2014, 15:30 | Сообщение # 2 |
|
Группа: Гости
| в треугольнике АВС проведена медиана ВМ и биссектриса АР. АС=3*АВ.
Найти отношение площади треугольника АКМ к площади четырехугольника КРСМ
|
| |
| |
| inf | Дата: Понедельник, 19.05.2014, 11:58 | Сообщение # 3 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Биссектриса угла М Δ MNK делит медиану NN1 в отношении 3 : 7, считая от вершины N. В каком отношении, считая от вершины К, эта биссектриса делит медиану КК1?
Решение:
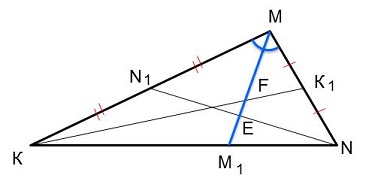
1) ММ1 - биссектриса ула М в Δ MNN1 ⇒ MN1 : MN = N1E : NE ⇒ MN1 : MN = 7 : 3 ⇒ 1/2MK : 2MK1 = 7 : 3 (т.к. NN1 и КК1 - медианы)⇒ MK : MK1 = 28 : 3
2) ММ1 - биссектриса ула М в Δ MКК1 ⇒ MК : MК1 = KF : FK1, но MK : MK1 = 28 : 3 ⇒ KF : FK1 = 28 : 3
Ответ: 28 : 3
|
| |
| |
| inf | Дата: Понедельник, 19.05.2014, 12:33 | Сообщение # 4 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Три окружности, радиусы которых 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трех окружностей.
Решение:
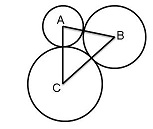
Пусть даны окр. (А; 2), окр. (В; 3), окр. (С; 10) ⇒ АВ = 5, ВС = 13, АС = 12.
Найдем площадь треугольника по формуле Герона S = √p(p - a)(p - b)(p - c)
S = 30.
С другой стороны, площадь треугольника через радиус вписанной окружности можно найти по формуле S = pr ⇒ r = 2.
Ответ: 2
|
| |
| |
| inf | Дата: Вторник, 20.05.2014, 07:24 | Сообщение # 5 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Диагонали четырехугольника АВСD, вершины которого расположены на окружности пересекаются в точке М. Известно, что ∠ АВС = 720, ∠ BCD = 1020, ∠ AMD = 1100 Найдите ∠ АСD.
Решение:
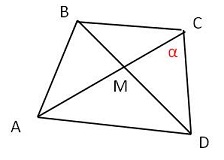
Обозначим для удобства искомый угол α, тогда ∠ АСВ = 1020 - α ⇒ ∠ BDA = 1020 - α (∠ АСВ = ∠ BDA как вписанные, опирающиеся на одну дугу); ∠ АBD = α
В Δ AMD ∠ MAD = 1800 - 1100 - 1020 + α = α - 320 ⇒ ∠ DВС = α - 320.
∠ АВС = 720 и ∠ АВС = ∠ АBD + ∠ DВС ⇒ α + α - 320 = 720 ⇒ 2α = 1040 ⇒ α = 520
Ответ: 520
|
| |
| |
| inf | Дата: Вторник, 20.05.2014, 07:43 | Сообщение # 6 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Сторона АВ треугольника АВС на 5√3 меньше его полупериметра, угол АВС равен 1200. Найдите радиус окружности, касающейся стороны ВС и продолжения сторон АВ и АС.
Решение:
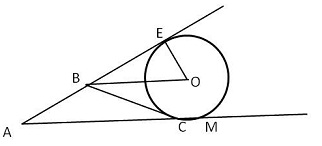
АЕ = АВ + ВЕ
АМ = АС + СМ
Почленно складывая два этих равенства, получим:
2АЕ = АВ + АС + ВС ⇒ АЕ = pАВС, и АВ на 5√3 меньше полупериметра Δ АВС ⇒ ВЕ = 5√3.
Окр (О; ОЕ) вписана в угол ЕВО ⇒ ВО - биссектнриса ⇒ ∠ ОВЕ = 300
Δ ВЕО - прямоугольный (ВЕ ⊥ ОЕ) ⇒ tg В = ОЕ/ОВ ⇒ 1/√3 = ОЕ/5√3 ⇒ ОЕ = 5.
Ответ: 5.
|
| |
| |
| inf | Дата: Вторник, 20.05.2014, 10:31 | Сообщение # 7 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Длина катета АС прямоугольного треугольника АВС равна 3 см. Окружность с диаметром АС пересекает гипотенузу АВ в точке М. Найдите площадь треугольника АВС, если известно, что АМ : МВ = 9 : 16.
Решение:

Пусть ∠ А = α ⇒ ∠ МОС = 2α (∠ А вписанный в данную окружность, ∠ МОС - центральный, опирающийся на ту же дугу) ⇒ ∠ АСМ = 900 - α (Δ СОМ - равнобедренный) ⇒ Δ АМС - прямоугольный.
Δ АМС и Δ АВС подобны ⇒ АС/АВ = АМ/АС.
Пусть АМ = 9х ⇒ ВМ = 16х ⇒ АВ = 25х
3/25х = 9х/3 ⇒ х = 0,2 ⇒ АВ = 5 ⇒ ВС = 4 (по т.Пифагора).
SABC = 1/2 FC*DC = 6.
Ответ: 6.
|
| |
| |
| inf | Дата: Воскресенье, 25.05.2014, 15:54 | Сообщение # 8 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В треугольнике АВС биссектриса ВЕ и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника АВС.
Решение:
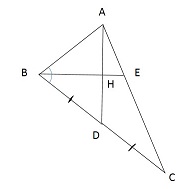
1) Δ АНВ ∼ Δ DНВ (∠ Н - прямой, ВЕ - биссектриса) ⇒ ∠ВАН = ∠BDН ⇒ Δ DВН - равнобедренный ⇒ АВ = BD и ВН - медиана ⇒ АН = 48, ВС = 2АВ и SАНВ = SDНВ
2) Т.к. ВЕ - биссектриса, то SABE/SCBE = AB/BC = 1/2 ⇒ AE/EC = 1/2 ⇒ AC = 3AE.
3) SABE = 1/2АН · ВЕ = 1/2 · 48 · 96 = 48 · 48
4) Т.к. AD - медиана, то
SABD = SADC
2SABH = SAHE + SHECD
2SABH = (SABE -SABH) + (SBEC - SBHD)
2SABH = SABE - SABH + 2SABE - SABH
4SABH = 3SABE
SABH = 3/4SABE = 3/4 · 48 · 48 = 3 · 48 · 48
С другой стороны SABH = 1/2 · АН · ВН = 1/2 · 48 · ВН ⇒ 1/2 · 48 · ВН = 3 · 48 · 48 ⇒ ВН = 72 ⇒ НЕ = 24.
5) Из Δ АВН АВ = √(АН2 + ВН2) = √(482 + 722) = 24√13 ⇒ ВС = 48√13.
5) Из Δ АЕН АЕ = √(АН2 + НЕ2) = √(482 + 242) = 24√5 ⇒ АС = 72√5.
Ответ: 24√13; 48√13; 72√5.
|
| |
| |
| inf | Дата: Понедельник, 26.05.2014, 17:19 | Сообщение # 9 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Цитата Гость ( 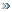 ) в треугольнике АВС проведена медиана ВМ и биссектриса АР. АС=3*АВ. Найти отношение площади треугольника АКМ к площади четырехугольника КРСМ
Решение:
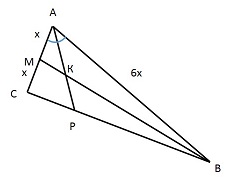
Пусть SABC = S.
Т.к. ВМ - медиана, то SAМB = SСМВ = 1/2 S.
Т.к. АР - биссектриса, то РС/ВР = 1/3 и МК/ВК = 1/6 ⇒ SAРС / SАВР = 1/3 и SAМК / SАВК = 1/6 ⇒ SAРС = 1/4 SABC = 1/4 S и SAМК = 1/6 SAМB = 1/12 S.
SКРСМ = SAРC - SAМК = 1/6 S.
SAМК / SКРСМ = 1/12 S : 1/6 S = 1/2.
Ответ: 1/2
|
| |
| |
| inf | Дата: Понедельник, 26.05.2014, 20:26 | Сообщение # 10 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В трапеции ABCD (AD || BC, AD > BC) на диагонали АС выбрана точка Е так, что BE || CD. Площадь треугольника АВС равна 10. Найдите площадь треугольника DEC.
Решение:
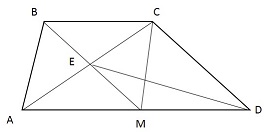
BMCD - параллелограмм (ВЕ ∩ AD = М)
SBMCD = 2SABC = 20 (имеют одинаковую высоту, проведенную к одному и тому же основанию ВС)
SDEC = 1/2 SBMCD = 10 (имеют одинаковую высоту, проведенную к одному и тому же основанию CD).
Ответ: 10
|
| |
| |
| inf | Дата: Среда, 28.05.2014, 14:58 | Сообщение # 11 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В остроугольном треугольнике АВС высоты, проведенные из вершин В и С продолжили до пересечения с описанной окружностью в точках В1 и С1. Найдите уголи ВАС если известно, что отрезок В1С1 проходит через центр окружности.
Решение:

1) Точки А, В, С, В1, С1 лежат на одной окружности (О - центр окружности, ОВ1 - радиус).
2) ВСВ1С1 - равнобедренная трапеция (∠ В1ВС1 = ∠ С1СВ1 = 900, т.к. опираются на диметр В1С1, Δ В1ВС1 = Δ СС1В1 и О - середина В1С1 ⇒ Δ АВС - равнобедренный (ОВ1 - ОВ радиусы) ⇒ О лежит на высоте, проведенной из вершины А, т.е. ∠ АОС1= 900, но ∠ АОС1 - центральный, а ∠ АСС1 - вписанный, опирающийся на ту же дугу АС1⇒ ∠ АСС1= 450
3) Δ АНС - прямоугольный (СН - высота) ⇒ ∠ НАС = 450
Ответ: 450
|
| |
| |
| inf | Дата: Среда, 28.05.2014, 18:38 | Сообщение # 12 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| вариант 101 от 31.05.2014 (источник)
Из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник ВСР, равен 60, тангенс угла ВАС равен 4/3. Найдите радиус окружности, вписанной в треугольник АВС.
Решение:
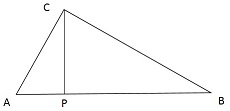
Пусть r - радиус окружности, вписанной в треугольник ВСР, R - радиус окружности, вписанной в треугольник АВС.
tg A = 4/3 ⇒ ВС/АС = 4/3 (тангенс - отношение противолежащего катета к прилежащему).
Т.е. ВС = 4х, АС = 3х ⇒ АВ = 5х (по теореме Пифагора)
Δ АВС ∼ Δ ВСР и ВС/АВ = 4/5 ⇒ в этом же отношении находятся и радиусы окружностей вписанных в эти треугольники, т.е. r/R = 4/5 ⇒ R = 75.
Ответ: 75
|
| |
| |
| inf | Дата: Суббота, 11.10.2014, 10:42 | Сообщение # 13 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| В трапеции ABCD углы A и D при основании AD соответственно равны 60o
и 30o
. Точка N лежит на основании BC, причём BN : NC = 2. Точка
M лежит на основании AD, прямая MN перпендикулярна основаниям
трапеции и делит её площадь пополам. Найдите отношение AM : MD
Решение:

1) ΔАВВ1: tgB = AB1/BB1 ⇒ tg300 = AB1/h ⇒ AB1= √3/3 · h
2) ΔDCC1: tgC = DC1/CC1 ⇒ tg600 = DC1/h ⇒ DC1= √3 · h
3) Т.к. прямая MN делит площадь трапеции пополам, то SABNM = SMNCD
Пусть NC = x, тогда BN = 2х, подставляем, выражаем х через h:
x = √3/3 · h
4) AM = AB1 + 2x = √3 · h
DM = DC1 + x = 4√3/3 · h
AM : MD = √3 · h / (4√3/3 · h) = 3/4
Ответ: 3/4
|
| |
| |
| Гость | Дата: Понедельник, 13.10.2014, 18:10 | Сообщение # 14 |
|
Группа: Гости
| В треугольнике АВС через вершину А проведена окружность касающаяся стороны ВС в вершине С и пересекающая сторону АВ в точке D.Найдите длину стороны АВ , если АD=16, и АС:СD=3:1
|
| |
| |
| inf | Дата: Пятница, 24.10.2014, 12:02 | Сообщение # 15 |
 Генерал-майор
Группа: Администраторы
Сообщений: 263
Статус: Offline
| Цитата Гость (  ) В треугольнике АВС через вершину А проведена окружность касающаяся стороны ВС в вершине С и пересекающая сторону АВ в точке D.Найдите длину стороны АВ , если АD=16, и АС:СD=3:1 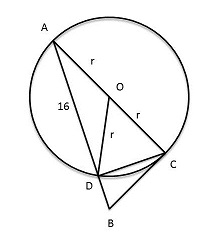
1) Т.к. окружность касается стороны ВС в вершине С, то треугольник АВС прямоугольный.
2) По теореме косинусов
c2 = a2 + b2 - 2ab · cos α,
∠AOD = α ⇒ ∠DОС = 1800 - α (cos(1800 - α) = cos α)
Δ AOD: AD2 = AO2 + OD2 - 2AO · OD · cos α
AD2 = r2 + r2 - 2r · r · cos α ⇒ cos α = (2r2 - AD2)/2r2
Δ COD: CD2 = CO2 + OD2 - 2CO · OD · cos (1800 -α)
CD2 = r2 + r2 + 2r · r · cos α ⇒ CD2 = 2r2 + 2r2 · (2r2 - AD2)/2r2 ⇒ CD2 = 4r2 - AD2 ⇒
AC2 = CD2 + AD2 ⇒ Δ ADC - прямоугольный.
Т.к. АС:СD=3:1 и AC2 = CD2 + AD2 ⇒ AC2 = 288
3) Δ АВС ∼ Δ ADС ⇒ АВ = АС2/AD ⇒ АВ = 18
Ответ: 18
|
| |
| |