Алгебраические дроби.
Определение: Алгебраической дробью называют выражение P/Q, где P и Q - многочлены, P - числитель алгебраической дроби, Q - знаменатель.
Алгебраическая дробь не имеет смысла при всех таких значениях переменных, при подстановки которых, знаменатель дроби обращается в ноль (равен нулю). Данные значения переменных называются недопустимыми, остальные значения - допустимыми значениями. Т.о. "найти значения переменных, при которых дробь не имеет смысла" или "найти множество недопустимых значений переменных" - это значит найти такие значения, при которых знаменатель равен нулю (приравнять знаменатель к нулю, решить полученное уравнение, записать найденные значения в ответ). Дробь имеет смысл тогда и только тогда, когда ее знаменатель не равен нулю, т.е. при каждом допустимом значении переменных. "Найти значения переменных, при которых дробь имеет смысл" или "найти область определения алгебраической дроби" - это значит найти множество допустимых значений переменных, т.е. исключить недопустимые (приравнять к нулю знаменатель, решить полученное уравнение, в ответ записать все значения переменных, кроме найденных).
Алгебраическая дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель нет. Для того, чтобы найти значения переменных, при которых дробь равна нулю, нужно: приравнять знаменатель к нулю, решить полученное уравнение; приравнять числитель к нулю, решить полученное уравнение; исключить значения переменных, совпадающие со значениями, полученными при решении первого уравнения.
Основное свойство алгебраической дроби.
1) И числитель и знаменатель алгебраической дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен или на одно и то же отличное от нуля число) - тождественное преобразование алгебраической дроби.
2) И числитель и знаменатель алгебраической дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен или на одно и то же отличное от нуля число) - тождественное преобразование алгебраической дроби, называемое сокращением алгебраической дроби.
Правила изменения знаков у числителя и/или знаменателя алгебраической дроби.
Можно поменять знаки одновременно у числителя и знаменателя. Если изменить знак только у чилителя или только у знаменателя, то нужно поменять знак и перед дробью.
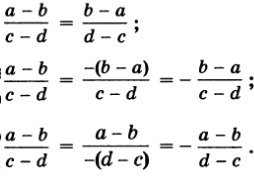
Алгоритм приведения алгебраических дробей к наименьшему общему знаменателю.
1. Разложить знаменатели на множители;
2. Домножить каждую дробь на все множители, входящие в разложение знаменателей других дробей, но не совпадающие со множителями этой дроби.






