
Взаимное расположение прямых и плоскостей в пространстве.
Способы определения плоскости.
Из аксиом стереометрии и их следствий получаем 4 способа задания плоскости.
Плоскость единственным образом может быть определена:
Через любые 3 точки пространства, не лежащие на одной прямой проходит плоскость, и при том только одна.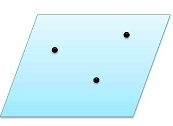 | Через прямую и не лежащую на ней точку проходит плоскость, и при том только одна. | Через две пересекающиеся прямые проходит плоскость, и при том только одна.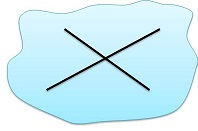 | Через две параллельные прямые проходит плоскость, и при том только одна. |

Параллельные прямые в пространстве.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной и при том только одна.
| Если одна из параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. | 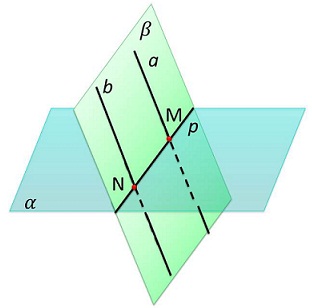 |
| Если две прямые параллельны третьей прямой, то они параллельны. | 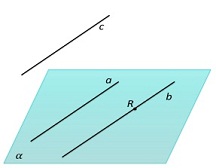 |
Взаимное расположение прямой и плоскости в пространстве.
| Общие точки | Взаимное расположение | |
 | Более одной | Прямая лежит в плоскости |
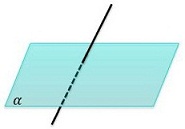 | Только одна | Прямая пересекает плоскость |
 | Ниодной | Прямая и плоскость параллельны |
Параллельность прямой и плоскости.
Признак параллельности прямой и плоскости:
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
| Если плоскость проходит через данную прямую, параллельнуй другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. | 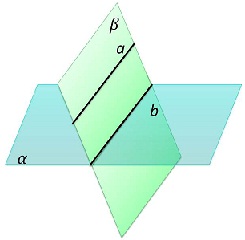 |
| Если одна из двух паралельных прямых параллельна, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. | 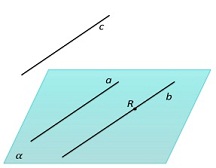 |








