Углы с сонаправленными сторонами. Угол между прямыми.
I Ответьте на вопросы, ответы внесите в форму ниже.
1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны? 2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться? б) быть скрещивающимися? 3. Могут ли скрещивающиеся прямые a и b быть параллельными прямой с? 4. Даны две скрещивающиеся прямые a и b. Точки А и А1 лежат на прямой a, точки В и В1 лежат на прямой b. Как будут расположены прямые АВ и А1В1? 5. Прямая a скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые a и с - скрещиваются? 6. Каково должно быть взаимное расположение трех прямых, чтобы можно провести плоскость, содержащую все прямые?
Любая прямая a, лежащая в плоскости, разделяет плоскость на 2 части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей. Два луча ОА и О1А1, лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной плоскости с границей ОО1. Два луча ОА и О1А1, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.
Теорема: Если стороны двух углов соответственно сонаправлены, то такие углы равны. | 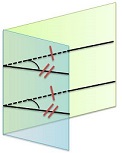 |
Дано: ∠ О и ∠ О1 с сонаправленными сторонами.Доказать: ∠ О = ∠ О1. Доказательство: На сторонах угла О отметим любые точки А и В и на соответственных сторонах угла О1 отметим точки А1 и В1 такие, что О1А1 = ОА и О1В1 = ОВ. 1. Рассмотрим ОАА1О1. | ОА || О1А1 | ⇒ ОАА1О1 - параллелограмм ⇒АА1 || ОО1 и ВВ1 = ОО1. | | ОА = О1А1 |
2. Рассмотрим ОВВ1О1. | ОА || О1В1 | ⇒ ОВВ1О1 - параллелограмм ⇒ВВ1 || ОО1 и ВВ1 = ОО1. | | ОА = О1В1 |
Вывод: AA1 || OO1 и ВВ1 || ОО1 ⇒ АА1 ||ВВ1; АА1 = ОО1 и ВВ1 = ОО1 ⇒ АА1 = ВВ1 ⇒ АА1ВВ1 - параллелограмм ⇒ АВ = А1В13. Рассмотрим Δ АВО и Δ А1В1О1. Δ АВО = Δ А1В1О1 по трем сторонам Вывод: ∠ О = ∠ О1 Углом между пересекающимися прямыми называется угол, не превосходящий любой из трех остальных (то есть наименьший из четырех образованных). Обратите внимание, что здесь подразумевается градусна ямера, а не геометрическая фигура. По определению угол 00 < α ≤ 900. 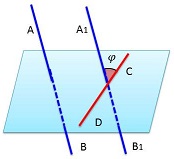 Угол между скрещивающимися прямыми АВ и CD определяется как угол между пересекающимися прямыми А1В1 и С1D1 соответственно паралельными АВ и CD.
Итак, для того чтобы найти угол между скрещивающимися прямыми, нужно через "удобную" точку провести параллельные прямые (для данных скрещивающихся) и найти угол между ними. Выбор "удобной" точки зависит от условия задачи, т.к. величина угла между скрещивающимися прямыми не зависит от выбора точки (по теореме о трех параллельных прямых и теореме об углах с сонаправленными сторонами).
Задачи: Рассмотрите параллелепипед ABCDA1B1C1D1 (ABCD - квадрат).
Угол между скрещивающимися прямыми D1C1 и ВС равен 900, т.к. равен углу между пересекающимися прямыми DC и ВС, DC || D1C1.
Угол между скрещивающимися прямыми А1В1 и АС равен 450 (объясните почему) | 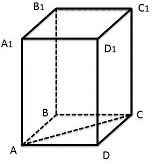 |
№ 44 Дано: OB || CD; ОA и CD скрещиваются; а) ∠ АОВ = 400; б) ∠ АОВ = 1350; в) ∠ АОВ = 900 Найти: угол между ОА и CD. Решение: а) ∠ АОВ = 400; CD || ОВ ⇒ угол между скрещивающимися прямыми ОА и CD равен 400 б) ∠ АОВ = 1350.Угол между пересекающимися прямыми ОА и ОВ равен: 1800 - 1350 = 450 ⇒ угол между скрещивающимися прямыми ОА и CD равен 450
Определение: Четырехугольник называетсяя пространственным, если его вершины не лежат в одной плоскости.
№ 43 Дано: ABCD - пространственный четырехугольник. L - середина АВ; К - середина ВС; N - середина DC; М - середина DA Доказать: LKNM - параллелограмм. Решение: 1) LK - средняя линия Δ АВС, LK = ½АС, LK || АС. 2) MN - средняя линия Δ АDС, MN = ½АС, MN || АС. 3) ML - средняя линия Δ АDB, LK = ½BD, ML || BD. 4) NK - средняя линия Δ CBD, NK = ½BD, NK || BD. 5) LK || MN, LK = MN; ML || NK, ML = NK ⇒ MNKL - параллелограмм.
№ 45 решите самостоятельно. Рисунок в помощь:
Д.з.: готовимся к диктанту - повторить теорию (новый материал выучить)
|